Relações Envolvendo Medidas de Ângulos e Lados dos Triângulos


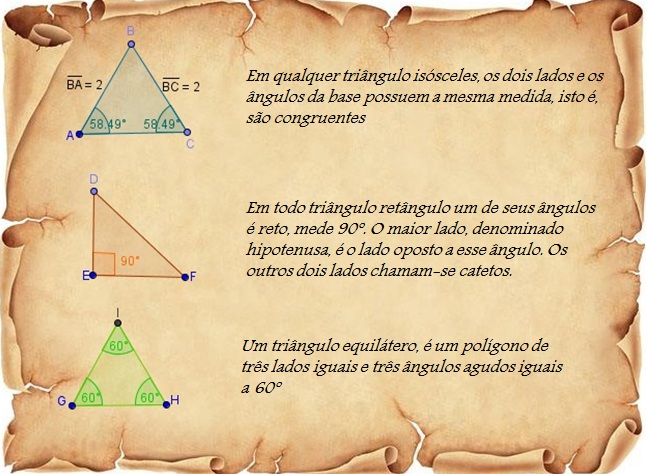


O teorema abaixo nos dá um resultado importante sobre as medidas dos ângulos internos de um triângulo.

A próxima relação diz respeito à soma dos ângulos externos.
O teorema que veremos agora confirma a investigação que fizemos no exercício anterior.
Nos exercícios a seguir você vai precisar, além das informações acima, de conhecimentos sobre ângulos formados por retas paralelas cortadas por uma reta transversal.
Caso você tenha se esquecido, ou ainda não tenha visto o assunto, abaixo vai um vídeo do youtube e um link com uma explicação complementar sobre o assunto.
8º Ano - Prog.11 - Feixe de Paralelas cortado por reta transversalVídeo editado para as aulas da Educopédia.(postado por Lucimar) http://www.youtube.com/watch?v=YpIOiHX1m7M
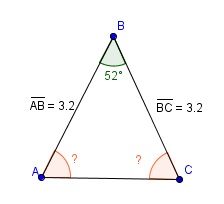
Observe o triângulo abaixo.
Sabendo que o ângulo
mede 52º , quais são as medidas dos ângulos
e
.
|
Os ângulos 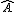 e e 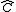 medem 63º cada um. medem 63º cada um.
| |
|
Os ângulos 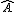 e e 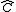 medem 64º. medem 64º.
| |
|
O ângulo 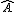 mede 63,95º e o ângulo mede 63,95º e o ângulo 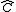 mede 64º. mede 64º.
| |
|
As informações dadas não são suficientes para determinar as medidas dos ângulos 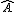 e e 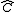 , portanto todas as respostas dadas estão erradas. , portanto todas as respostas dadas estão erradas.
|
Observe a figura abaixo e complete a frase com a resposta correta.
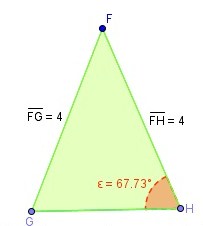
a) O triângulo FGH é porque dois de seus lados tem a mesma medida.
b) Num triângulo isósceles os ângulos da base tem medidas .
c) A medida do ângulo oposto ao lado GH é .
Marcos e João estão jogando bilhar.
Antes de iniciar o jogo eles se desafiaram. Combinaram que a última bola de cada um só poderia ser colocada na caçapa 1.
A figura abaixo mostra a disposição das últimas bolas. A vermelha é de Marcos e a verde de João.
Está na vez de Marcos fazer sua jogada. Ele analisou a situação e achou que a melhor maneira de vencer o jogo era, com uma única tacada na bola branca, acertar a vermelha de tal forma que ela fizesse um ângulo 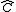 com a borda da mesa, a caçapa e a posição inicial da branca como mostra a figura.
com a borda da mesa, a caçapa e a posição inicial da branca como mostra a figura.
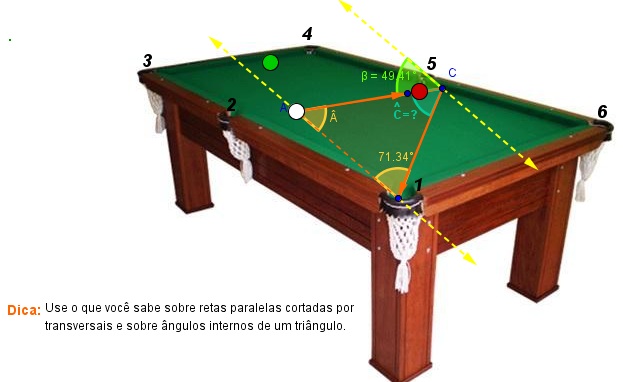
Analise bem a figura e determine a medida do ângulo 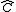 .
.
Suponha que Marcos tenha errado a tacada e que as bolas bateram umas nas outras e mudaram de posição.
Então João vai ter sua oportunidade de vencer o jogo.
Analise as posições das bolas branca e verde e desenvolva uma estratégia geométrica para que João consiga colocar a bola dele na caçapa um com uma única tacada, ou que a bola verde possa ao menos ficar o mais próximo possível da caçapa 1.
Em seguida determine o ângulo que a bola verde fez com a borda da mesa para entrar na caçapa.
Sua estratégia pode ser feita no applet abaixo.
Não se esqueça de que você só pode usar triângulos e seus conhecimentos sobre ângulos em retas paralelas cortadas por transversais.
Faça sua estratégia geométrica, determine o ângulo que a bola verde vai fazer com a borda da mesa, a caçapa1 e a bola branca e imprima seu desenho.
Este artigo está licenciado segundo Creative Commons Attribution 3.0 License