Ortocentro

- Identificar as posições relativas de duas retas em um plano;
- Definir retas perpendiculares;
- Definir altura relativa a um lado de um triângulo;
- Encontrar as alturas de um triângulo.
Você se lembra que posições uma reta pode ocupar em um plano?
Mas, antes de entrar nesse assunto, o que é plano mesmo, hein?
Então, podemos considerar uma folha de seu caderno como uma parte de um plano.
Observe que ela tem altura e comprimento, ou seja, duas dimensões.
No caso do plano, de um modo geral, sua altura é infinita e seu comprimento também.
Voltando à folha de seu caderno, observe suas linhas. Como elas estão dispostas?
A formas como as linhas da folha de seu caderno estão dispostas representa uma das posições relativas de duas retas, ou mais, num plano: dizemos que elas são paralelas.
Você se lembra que outras posições elas podem ocupar no plano?
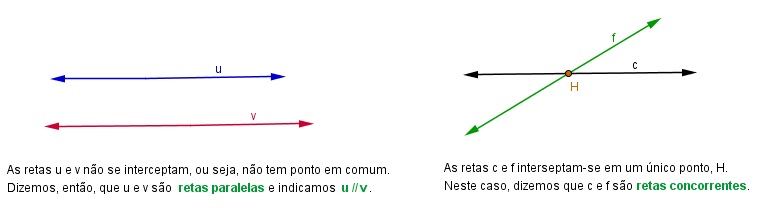
A figura abaixo mostra duas delas.
Além destas duas posições temos, ainda, as retas coincidentes. Dizemos que duas retas são coincidentes quando elas pertencem ao mesmo plano e possuem todos os pontos em comum.
Observe que, se s e t são retas coincidentes, elas possuem todos os pontos em comum. Isto quer dizer que r e s representam uma única reta, são iguais.

![]()
Você já viu que duas retas num mesmo plano podem ser paralelas, concorrentes e coincidentes(neste caso elas representam a mesma reta).
Sabemos que duas retas são concorrentes se elas se interseptam num único ponto. Mas existe um tipo especial de retas concorrentes: são as retas perpendiculares.
Elas interseptam-se num único ponto, mas possuem uma propriedade especial.
É isso que vamos ver na definição a seguir:

OBS: Como o ângulo formado entre r e s é reto, isto é, mede 90º, dizemos que r e s são perpendiculares e indicamos
.

![]()
Quando falamos de altura, imaginamos a medida de uma pessoa, de uma parede, de um muro,...
Mas, e quando falamos da altura de um triângulo? Você seria capaz de formar uma imagem, ou uma definição dessa expressão?
Vamos ver uma boa definição para altura de um triângulo.
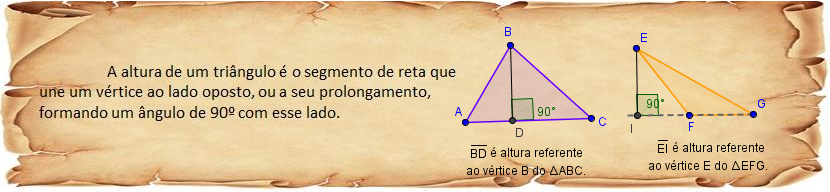
Agora que já sabemos a definição formal de altura de um triângulo, vamos visualizar o significado disso através da construção.
Vamos ver um vídeo que mostra o que é graficamente essa altura e como encontrá-la utilizando o Geogebra.

Este artigo está licenciado segundo Creative Commons Attribution 3.0 License